Skip to content
SplashKit
Announcements

Vector Magnitudes

Understanding vector magnitudes, squared magnitudes, and inversions is essential for various programming applications, from game mechanics to physics simulations. This tutorial explores these concepts using SplashKit functions to enhance your programming toolkit.
Written by:
Last updated: 08 Dec 24

While some Python code has been included in basic functions, full Python code for this tutorial is still in development.

Vector Magnitudes

Vectors are used in programming to represent quantities that involve direction and magnitude. Understanding how to compute and use vector magnitudes is essential for many tasks, such as movement calculations and physics simulations. This tutorial will guide you through these concepts using SplashKit functions.

SplashKit Vector Functions Used in This Tutorial

  1. Vector Magnitude
  2. Vector Magnitude Squared
  3. Vector Invert

Vector Magnitude

The magnitude of a vector represents its length or size in space. It is calculated as the distance from the origin to the vector’s point. In a 2D space, the magnitude gives you a measure of how “long” or “strong” the vector is.

If a vector represents velocity, the magnitude indicates the speed; if it represents force, the magnitude shows the strength of the force applied. For a 2D vector (x, y), the magnitude is calculated using the formula:

The magnitude provides a scalar value that reflects how “intense” or “strong” the vector is, without considering its direction.

Vector Magnitude Squared

vector_magnitude_squared is calculated using the formula:

When comparing the lengths of two vectors, you only need to compare their magnitude squared values. This eliminates the need for square root calculations and speeds up the comparison process. In some performance-critical applications, calculating the magnitude squared value is often more computationally efficient than calculating the magnitude itself, due to it avoiding the computationally expensive square root operation.

When Not To Use Magnitude Squared to Compare?

While both vector_magnitude and vector_magnitude_squared have the same theoretical time complexity, the square root operation in the magnitude calculation is generally more computationally intensive than addition or multiplication. In practical terms, calculating the magnitude will typically take longer due to the square root operation.

While the magnitude squared value is efficient for comparisons, it is less intuitive for humans to interpret compared to the actual magnitude of a vector. For displaying and understanding vector lengths in a graphical context, the actual magnitude is usually more meaningful and easier to comprehend.

Vector Invert

vector_invert flips the direction of the vector while keeping its magnitude unchanged. This function is useful in various programming scenarios where you need to reverse the direction of movement or force.

In games or simulations, you might need to reverse the direction of movement or force. For example, if an object is moving in a certain direction and you want it to move in the exact opposite direction, you can use vector inversion.

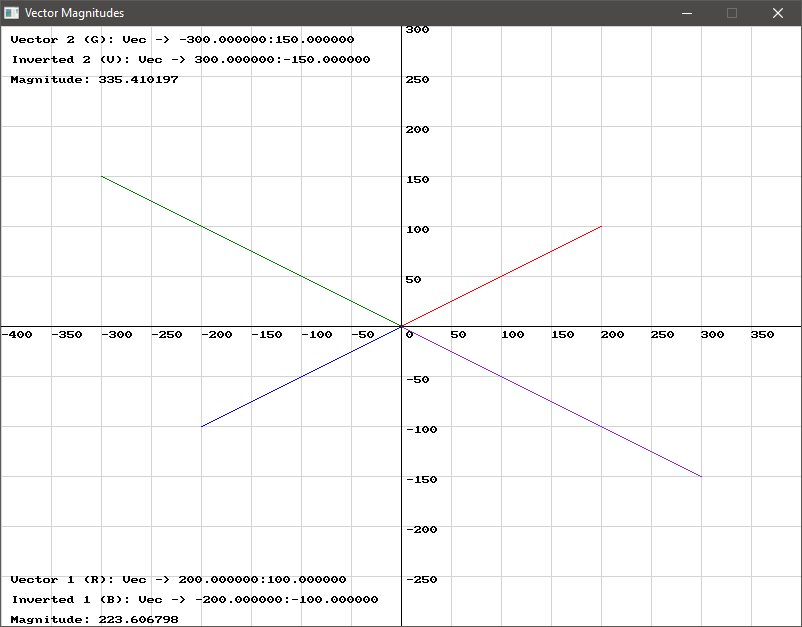
Visualising Magnitudes

The below diagram (and code) graphically represents two vectors and their respective inverse.

vector_2d my_vector_1;
my_vector_1.x = 200;
my_vector_1.y = 100;
vector_2d inverted_my_vector_1 = vector_invert(my_vector_1);

Vector 1 (my_vector_1):

  • This vector has coordinates (200, 100) and is drawn in red.
  • Its inverse, with coordinates (-200, -100), is drawn in blue.
  • Note how the x and y of the inverse is just the negative value of my_vector_1.

Vector 2 (my_vector_2):

  • This vector has coordinates (-300, 150) and is drawn in green.
  • Its inverse, with coordinates (300, -150), is drawn in violet.
  • Note how the x and y of the inverse is just the negative value of my_vector_2.

Vector Magnitudes

Use this code in your own IDE to play with the functions for yourself! 
#include "splashkit.h"


using std::to_string;


const int GRID_SPACING = 50;


void draw_cartesian_grid()
{
    // Draw vertical lines and labels
    for (int x = 0; x < screen_width(); x += GRID_SPACING)
    {
        draw_line(COLOR_LIGHT_GRAY, x, 0, x, screen_height());
        if (x != screen_width() / 2) // Avoid overlapping with the y-axis label
        {
            draw_text(to_string(x - screen_width() / 2), COLOR_BLACK, x, screen_height() / 2 + 5);
        }
    }


    // Draw horizontal lines and labels
    for (int y = 0; y < screen_height(); y += GRID_SPACING)
    {
        draw_line(COLOR_LIGHT_GRAY, 0, y, screen_width(), y);
        if (y != screen_height() / 2) // Avoid overlapping with the x-axis label
        {
            draw_text(to_string(screen_height() / 2 - y), COLOR_BLACK, screen_width() / 2 + 5, y);
        }
    }


    // Draw x-axis and y-axis
    draw_line(COLOR_BLACK, 0, screen_height() / 2, screen_width(), screen_height() / 2); // x-axis
    draw_line(COLOR_BLACK, screen_width() / 2, 0, screen_width() / 2, screen_height());   // y-axis


    // Label the origin
    draw_text("0", COLOR_BLACK, screen_width() / 2 + 5, screen_height() / 2 + 5);
}


int main()
{
    open_window("Vector Magnitudes", 800, 600);


    // Define vectors
    vector_2d my_vector_1;
    my_vector_1.x = 200;
    my_vector_1.y = 100;


    vector_2d my_vector_2;
    my_vector_2.x = -300;
    my_vector_2.y = 150;


    // Define the origin (centre of the window)
    point_2d origin;
    origin.x = 400;
    origin.y = 300;


    // Calculate magnitudes
    double my_vector_1_magnitude = vector_magnitude(my_vector_1);
    double my_vector_2_magnitude = vector_magnitude(my_vector_2);


    // Invert vectors
    vector_2d inverted_my_vector_1 = vector_invert(my_vector_1);
    vector_2d inverted_my_vector_2 = vector_invert(my_vector_2);


    // Main loop
    while (!window_close_requested("Vector Magnitudes"))
    {
        process_events();
        clear_screen(COLOR_WHITE);


        // Draw Cartesian grid
        draw_cartesian_grid();


        // Draw the vectors as lines from the center of the screen
        draw_line(COLOR_RED, origin.x, origin.y, origin.x + my_vector_1.x, origin.y - my_vector_1.y);
        draw_line(COLOR_BLUE, origin.x, origin.y, origin.x + inverted_my_vector_1.x, origin.y - inverted_my_vector_1.y);
        draw_line(COLOR_GREEN, origin.x, origin.y, origin.x + my_vector_2.x, origin.y - my_vector_2.y);
        draw_line(COLOR_BLUE_VIOLET, origin.x, origin.y, origin.x + inverted_my_vector_2.x, origin.y - inverted_my_vector_2.y);


        // Display vector properties on the screen
        draw_text("Vector 2 (G): " + vector_to_string(my_vector_2), COLOR_BLACK, 10, 10);
        draw_text("Inverted 2 (V): " + vector_to_string(inverted_my_vector_2), COLOR_BLACK, 10, 30);
        draw_text("Magnitude: " + to_string(my_vector_2_magnitude), COLOR_BLACK, 10, 50);


        draw_text("Vector 1 (R): " + vector_to_string(my_vector_1), COLOR_BLACK, 10, 550);
        draw_text("Inverted 1 (B): " + vector_to_string(inverted_my_vector_1), COLOR_BLACK, 10, 570);
        draw_text("Magnitude: " + to_string(my_vector_1_magnitude), COLOR_BLACK, 10, 590);


        refresh_screen(60);
    }


    return 0;
}

Conclusion

Key take aways:

  • Magnitudes: Reflect the length of vectors and are always positive. Inverted vectors have the same magnitudes as the original vectors.
  • Comparison: Direct magnitude comparison indicates the relative lengths of vectors.
  • Magnitude Squared: Useful for comparisons to avoid the computational cost of square roots, retaining the same order of length comparison.